|
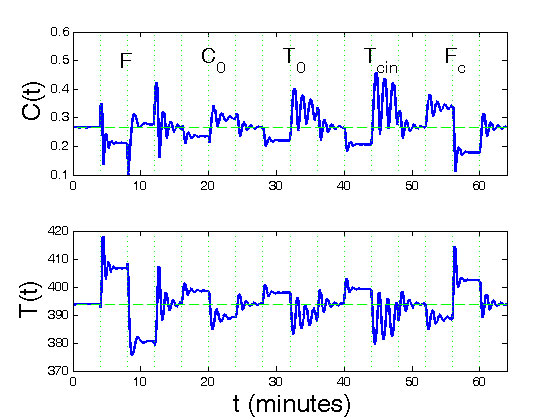
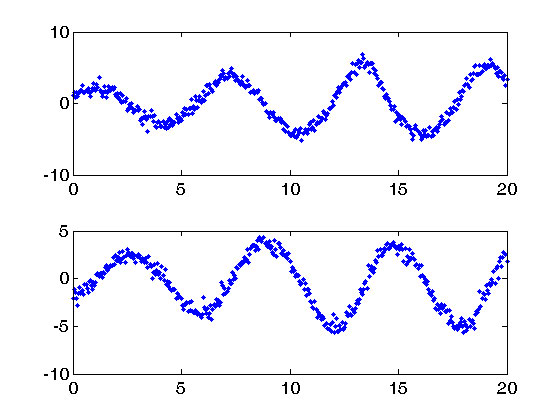
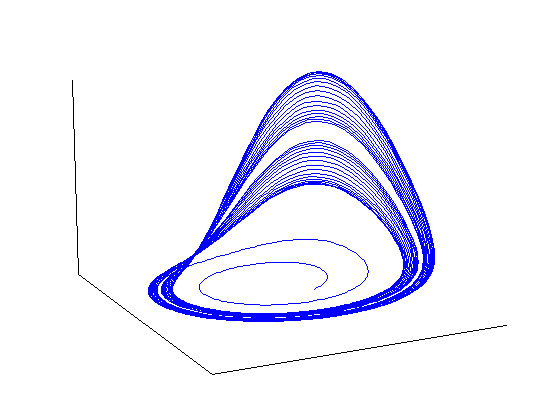
The term "dynamic system" typically implies a mathematical model expressed by a system of nonlinear differential or difference equations. Models of this nature have had a very long history in the physical sciences. More recently, these models have been employed for new areas such as clinical medicine, ecology, neurophysiology and the social sciences. There is, in addition, more and more attention given to assessing how well these models fit measured data in addition to displaying characteristics of the system being modeled at a qualitative level.
Statisticians have played a relatively limited role in these developments, in part because methods for fitting data with models of this nature that could spin off approaches to testing hypotheses and supplying confidence intervals for estimated quantities have not been easy to develop. Consequently, we have proposed this workshop as a means of bringing those working with dynamic models together with statisticians so as to stimulate further development, collaboration and application of statistical methodology in this important area.
Workshop Outline
The workshop will consist of 90 minute seminars with the intention that this will provide time to allow speakers to communicate ideas to a diverse audience and to foster extended questioning and discussion. In addition, a computer laboratory which can accommodate up to sixty people may be reserved by speakers and others for interactive demonstrations of software, data and models. Poster sessions will also be held between speakers and we strongly encourage contributions detailing methods, case studies and data.
This workshop will be partly funded by MITACS.
|