Les applications médicales
des fractales

L'auteur

Fahima Nekka est chercheure à la faculté de pharmacie de l'Université de Montréal.

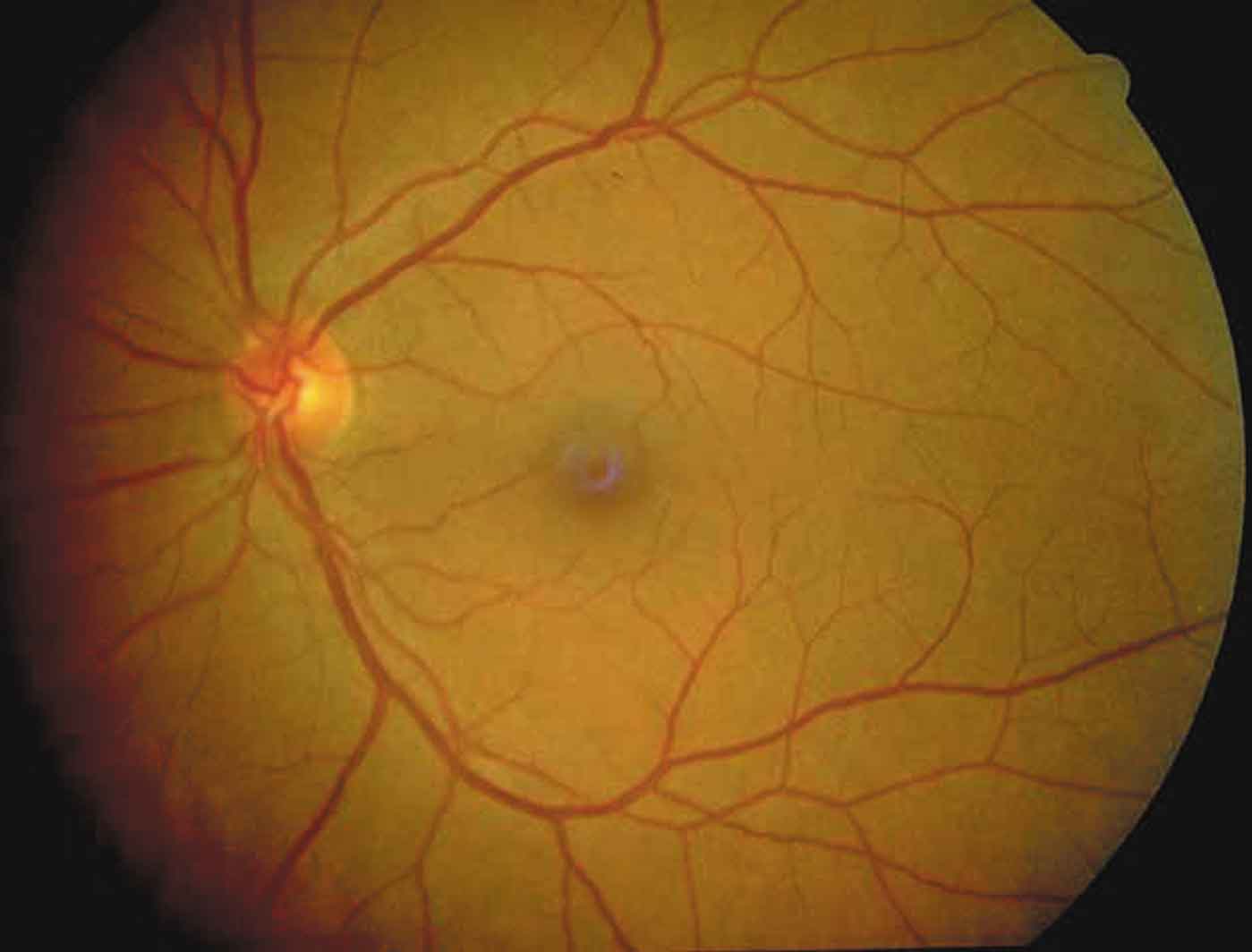
Les concepts de la géométrie fractale commencent à être utilisés en anatomie microscopique. Récemment, une méthode de détection du cancer du sein fondée sur les propriétés des structures fractales a été proposée. Le diagnostic d'un tel cancer est souvent basé sur des évaluations morphologiques par le pathologiste des propriétés physiques des cellules, telles que la taille, la forme, la régularité et l'apparence de la chromatine. Cette substance, présente sous forme de granules dans le noyau de la cellule, est formée d'ADN et de protéines. Pour établir son diagnostic, le pathologiste doit, entre autres, évaluer dans les cellules prélevées sur un tissu suspect, la présence de vides dans la chromatine, son apparence (est-elle fine ou grossière ?) et son aspect (est-elle regroupée ou éparse ?). Or la part de subjectivité de ces critères rend difficile un diagnostic certain.

Andrew Einstein et ses collaborateurs ont développé une méthode de diagnostic plus objective, qui exploite les propriétés fractales de ces aspects morphologiques des cellules du sein. L'irrégularité du noyau, qui est observée de manière subjective par le pathologiste, a pu être quantifiée à l'aide de deux dimensions fractales. D'autre part, les cellules se distinguent entre autres par l'existence de vides dans la chromatine. L'irrégularité et la taille de ces vides est un signe de malignité du cancer. Il existe un paramètre fractal, la lacunarité, qui décrit la distribution des vides dans une structure.

Armé de ces paramètres objectifs, l'équipe d'Einstein a réalisé une étude sur un groupe de 41 femmes. Le diagnostic basé sur l'approche fractale s'est avéré correct dans 95 % des cas.

En pharmacologie

La géométrie fractale a été introduite en technologie pharmaceutique, particulièrement grâce au professeur R. Tawachi de la faculté de pharmacie de l'Université de Montréal. Il a été parmi les premiers à l'utiliser pour étudier certains problèmes pharmaceutiques liés à la sélection des produits de base et à l'évaluation de la performance des procédés impliqués dans leur fabrication.

Les opérations des procédés de synthèse impliquées dans la production des poudres pharmaceutiques (telles que la cristallisation, la granulation, le tamisage et le séchage) peuvent influencer la forme et la surface des cristaux de la poudre. Ces changements morphologiques peuvent à leur tour affecter les propriétés physico-chimiques et mécaniques du produit final (telles que la dissolution, la réactivité chimique et le tassement). La caractérisation physique des poudres pharmaceutiques est donc une étape importante dans les procédés qui précèdent la mise en forme d'un médicament. L'approche fractale a contribué à établir le lien entre les irrégularités de surface des cristaux et la qualité du médicament.

Les maladies de l'oeil

Les pathologies de l'oeil engendrent des changements morphologiques de la structure vasculaire : le réseau des vaisseaux sanguins qui le parcourent se transforme. Les schémas de classification actuels se basent sur ces changements structuraux comme critères de détection et d'aide au diagnostic. L'évaluation de ces changements fait évidemment appel au jugement du pathologiste. Dans le cas des rétinopathies diabétiques (une affection de la rétine chez les diabétiques), l'analyse fractale a pu être utilisée avec succès. Elle a été employée comme moyen objectif de classification des changements morphologiques induits par la maladie, donnant ainsi au praticien un outil de diagnostic plus précis.

La géométrie fractale est utilisée avec succès dans le domaine biomédical. Elle procure au pathologiste des outils mathématiques pour quantifier ce qui jusque-là était difficilement mesurable. Au-delà du rôle descriptif et quantitatif de ces outils, leur capacité d'établir le lien entre la structure et la fonction d'un objet, et d'élucider les mécanismes impliqués, suscite un grand espoir.