Centre de recherches mathématiques

La petite galerie du CRM

A Finite Volume Extension of the
Lax-Friedrichs and Nessyahu-Tadmor Schemes for
Conservation Laws on Unstructured Grids

This page: 73 Kb. approx.

The non-oscillatory central difference scheme of Nessyahu and Tadmor, in which the resolution of Riemann problems at the cell interfaces is by-passed thanks to the use of the staggered Lax-Friedrichs scheme, is extended here to a two-step, two-dimensional non-oscillatory centered scheme in finite volume formulation. The construction of the scheme rests on a finite volume extension of the Lax-Friedrichs scheme, in which the finite volume cells are the barycentric cells constructed around the nodes of an FEM triangulation, for odd time steps, and some quadrilateral cells associated with this triangulation, for even time steps.

Piecewise linear cell interpolants using least-squares gradients combined with a van Leer-type slope limiting allow for an oscillation-free second-order resolution.

The method is illustrated by an air flow calculation around a 2-D double ellipse; and airfoil NACA0012. For more detail see [1], [2], [3].

The authors will now focus their efforts on applications to problems with the Navier-Stokes equations in conservation form for compressible flows [4] and three-dimensional transonic and supersonic flow problems (see Figure 2).

Aziz Madrane, Paul Arminjon

Fig. 1
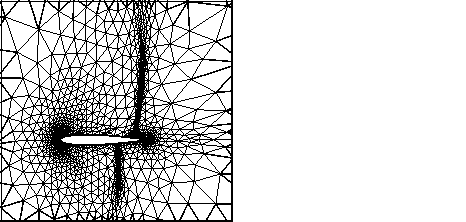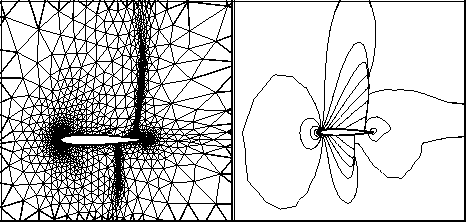
Figure 1
Mesh (4318 vertices) and Mach contours (Machinfinity = 0.85 and 1° of attack)

Fig. 2
Figure 2
3-D mesh

Fig. 3
Figure 3
Euler flow around a double ellipse. Original grid, barycentric cells Ci and quadrilateral cells Lij

Fig. 4
Figure 4
Double ellipse: Initial mesh (1558 vertices) and solution (pressure and Mach contours)

Fig. 5
Figure 5
Double ellipse: Final mesh (5055 vertices) and solution (pressure and Mach contours)

Fig. 6
Figure 6
Cp and Mach body cuts for this contribution

References

  1. P. Arminjon, M.C. Viallon and A. Madrane
    From Lax-Friedrichs to a multi-dimensional finite volume extension of the Nessyahu-Tadmor scheme for compressible flows
    Proc. Int. Conf. on Numerical Methods for the Euler and Navier-Stokes Equations, Centre de recherches mathématiques, Montréal, September 14-16, 1995, P. Arminjon and A. Dervieux, editors. To be published in the AMS-CRM Series.
  2. P. Arminjon ,M.C. Viallon A.Madrane (1996).
    A finite volume extension of the Lax-Friedrichs and Nessyahu-Tadmor scheme for Conservation Laws on unstructured grids
    CRM-2457 (abstract, résumé), Int. J. for Comp. Fluid Dynamics.
  3. P. Arminjon, A. Madrane, H. Kaddouri and M.C. Viallon
    Discontinuous finite elements and a 2-dimensional finite volume generalization of the Lax-Friedrichs and Nessyahu-Tadmor schemes for compressible flows on unstructured grids
    to appear in CFD Review, John Wiley, 1997, M.Hafez and K.Oshima, Editors.
  4. A. Madrane and P. Arminjon
    Non-Oscillatory Central Schemes for compressible 2-D Navier-Stokes equations using unstructured meshes
    En préparation.

Table des matières de la petite galerie du CRM

28 January 1998, webmaster@CRM.UMontreal.CA