The purpose of this study is to solve the Euler equations for compressible flow with discontinuous finite element method. The method is designed to work on structured as well as on unstructured meshes.The conservatives variables are approximated by discontinuous piecewise linears or bilinears. Mass balance is written for the discretization cells and numerical fluxes across the edges are calculated by using a one-dimensional Riemann solver in normal direction. The procedure is stabilized through a truly multidimensional slope limiter. The method is illustrated by an air flow calculation around a double ellipse at high Mach number.
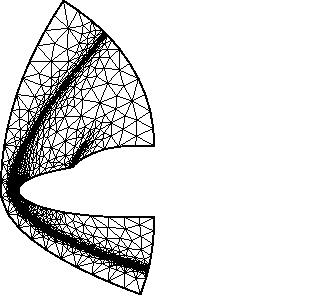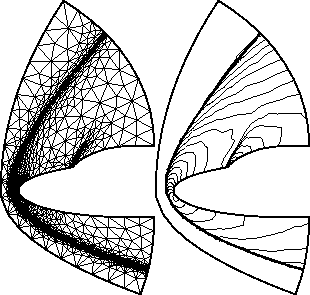
Figure 1
Mesh (2218 vertices) and Mach contour lines at hypersonic regime
(Mach
= 8.15 and 30° of attack)
Table des matières de la petite galerie du CRM
28 April 1998, webmaster@CRM.UMontreal.CA